笛卡尔树
引入
笛卡尔树是一种二叉树,每一个节点由一个键值二元组  构成。要求
构成。要求  满足二叉搜索树的性质,而
满足二叉搜索树的性质,而  满足堆的性质。如果笛卡尔树的
满足堆的性质。如果笛卡尔树的  键值确定,且
键值确定,且  互不相同,
互不相同, 也互不相同,那么这棵笛卡尔树的结构是唯一的。如下图:
也互不相同,那么这棵笛卡尔树的结构是唯一的。如下图:
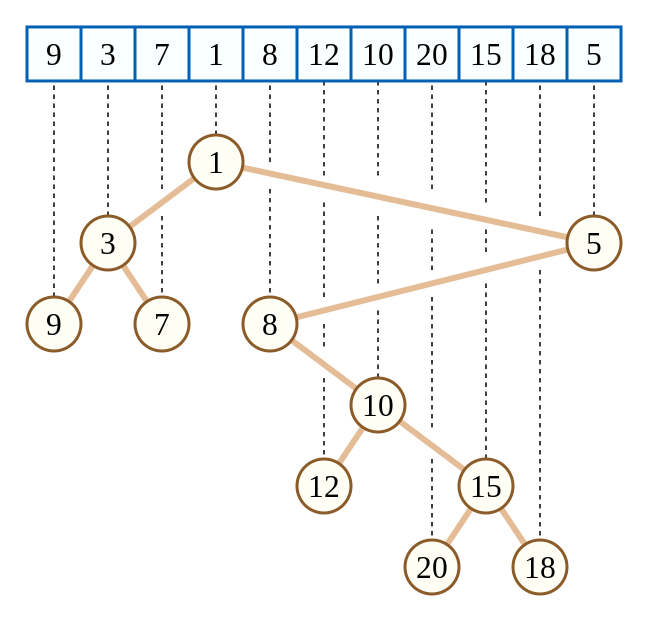
(图源自维基百科)
上面这棵笛卡尔树相当于把数组元素值当作键值  ,而把数组下标当作键值
,而把数组下标当作键值  。可以发现,这棵树的键值
。可以发现,这棵树的键值  满足二叉搜索树的性质,而键值
满足二叉搜索树的性质,而键值  满足小根堆的性质。同时根据二叉搜索树的性质,可以发现这种特殊的笛卡尔树满足一棵子树内的下标是一个连续区间。
满足小根堆的性质。同时根据二叉搜索树的性质,可以发现这种特殊的笛卡尔树满足一棵子树内的下标是一个连续区间。
竞赛中使用笛卡尔树时,常用数组下标作为二元组的键值  。
。
用栈构建笛卡尔树
过程
我们考虑将元素按下标顺序依次插入到当前的笛卡尔树中。那么每次我们插入的元素必然在这棵树的右链(右链:即从根节点一直往右子树走,经过的节点形成的链)的末端。于是我们执行这样一个过程,从下往上比较右链节点与当前节点  的
的  ,如果找到了一个右链上的节点
,如果找到了一个右链上的节点  满足
满足  ,就把
,就把  接到
接到  的右儿子上,而
的右儿子上,而  原本的右子树就变成
原本的右子树就变成  的左子树。
的左子树。
图中红框部分就是我们始终维护的右链:
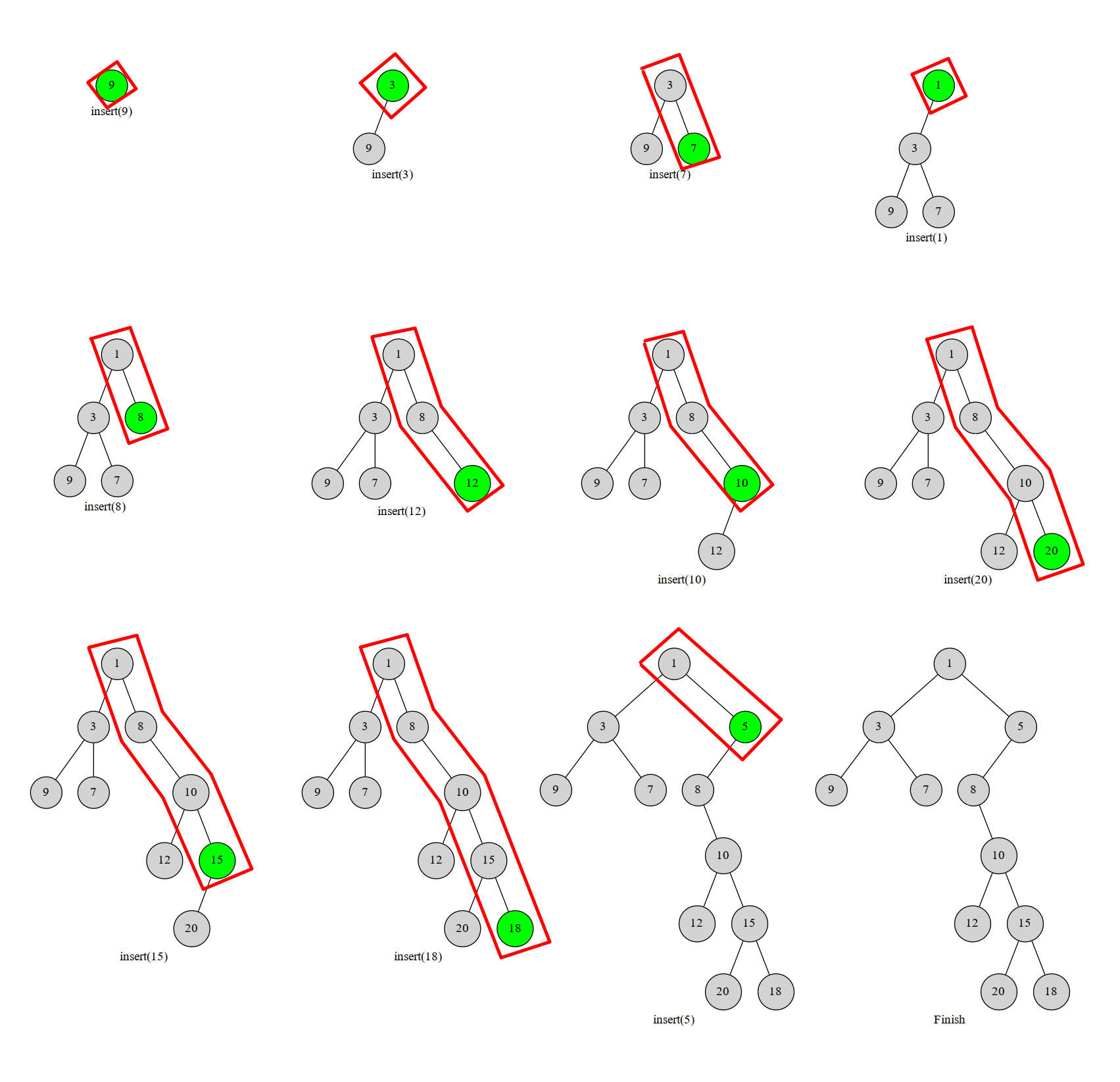
显然每个数最多进出右链一次(或者说每个点在右链中存在的是一段连续的时间)。这个过程可以用栈维护,栈中维护当前笛卡尔树的右链上的节点。一个点不在右链上了就把它弹掉。这样每个点最多进出一次,复杂度  。
。
笛卡尔树与 Treap
实际上,Treap 是笛卡尔树的一种,只不过 Treap 中  的值完全随机。Treap 有线性的构建算法,如果提前将键值
的值完全随机。Treap 有线性的构建算法,如果提前将键值  排好序,是可以使用上述单调栈算法完成构建过程的,只不过很少会这么用。
排好序,是可以使用上述单调栈算法完成构建过程的,只不过很少会这么用。
C++ 实现
| // stk 维护笛卡尔树中节点对应到序列中的下标
for (int i = 1; i <= n; i++) {
int k = top; // top 表示操作前的栈顶,k 表示当前栈顶
while (k > 0 && w[stk[k]] > w[i]) k--; // 维护右链上的节点
if (k) rs[stk[k]] = i; // 栈顶元素.右儿子 := 当前元素
if (k < top) ls[i] = stk[k + 1]; // 当前元素.左儿子 := 上一个被弹出的元素
stk[++k] = i; // 当前元素入栈
top = k;
}
|
例题
HDU 1506. Largest Rectangle in a Histogram
 个位置,每个位置上的高度是
个位置,每个位置上的高度是  ,求最大子矩形。如下图:
,求最大子矩形。如下图:
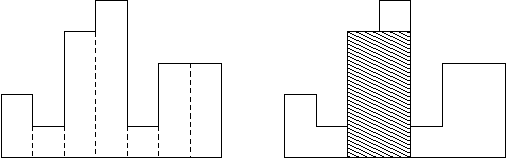
阴影部分就是图中的最大子矩阵。
解题思路
具体地,我们把下标作为键值  ,
, 作为键值
作为键值  满足小根堆性质,构建一棵
满足小根堆性质,构建一棵  的笛卡尔树。
的笛卡尔树。
这样我们枚举每个节点  ,把
,把  (即节点
(即节点  的高度
的高度  )作为最大子矩阵的高度。由于我们建立的笛卡尔树满足小根堆性质,因此
)作为最大子矩阵的高度。由于我们建立的笛卡尔树满足小根堆性质,因此  的子树内的节点的高度都大于等于
的子树内的节点的高度都大于等于  。而我们又知道
。而我们又知道  子树内的下标是一段连续的区间。于是我们只需要知道子树的大小,然后就可以算这个区间的最大子矩阵的面积了。用每一个点计算出来的值更新答案即可。显然这个可以一次 DFS 完成,因此复杂度是
子树内的下标是一段连续的区间。于是我们只需要知道子树的大小,然后就可以算这个区间的最大子矩阵的面积了。用每一个点计算出来的值更新答案即可。显然这个可以一次 DFS 完成,因此复杂度是  的。
的。
参考实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 | #include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
using ll = long long;
constexpr int N = 100000 + 10, INF = 0x3f3f3f3f;
struct node {
int idx, val, par, ch[2];
friend bool operator<(node a, node b) { return a.idx < b.idx; }
void init(int _idx, int _val, int _par) {
idx = _idx, val = _val, par = _par, ch[0] = ch[1] = 0;
}
} tree[N];
int root, top, stk[N];
ll ans;
int cartesian_build(int n) { // 建树,满足小根堆性质
for (int i = 1; i <= n; i++) {
int k = i - 1;
while (tree[k].val > tree[i].val) k = tree[k].par;
tree[i].ch[0] = tree[k].ch[1];
tree[k].ch[1] = i;
tree[i].par = k;
tree[tree[i].ch[0]].par = i;
}
return tree[0].ch[1];
}
int dfs(int x) { // 一次dfs更新答案就可以了
if (!x) return 0;
int sz = dfs(tree[x].ch[0]);
sz += dfs(tree[x].ch[1]);
ans = max(ans, (ll)(sz + 1) * tree[x].val);
return sz + 1;
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n, hi;
while (cin >> n, n) {
tree[0].init(0, 0, 0);
for (int i = 1; i <= n; i++) {
cin >> hi;
tree[i].init(i, hi, 0);
}
root = cartesian_build(n);
ans = 0;
dfs(root);
cout << ans << '\n';
}
return 0;
}
|
参考资料
笛卡尔树 - 维基百科
本页面最近更新:2024/7/30 18:20:55,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:Enter-tainer, ouuan, sshwy, StudyingFather, AngelKitty, GavinZhengOI, HeRaNO, iamtwz, Ir1d, jimmyas, kenlig, ksyx, littleyinhee, megakite, mgt, ouuan, zhouyuyang2002
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用


